01/05/2016
In this article we will focus on building our background up, so we can move to the fun stuff. First we review base 10 standard arithmetic, we use that to build the concept of base 2 or binary. Finally we show how the computer uses base 2 in multiple ways including to represent color values, IP networks and logic.
Common Math
In our everyday lives, we count with a number system called base 10. Essentially this means that we have the option of 0-9 (10 possibilities) in each place location and that each location represents a 10th powers. This is where the thousandths, hundredths and ones place comes from in basic arithmetic. An example is the integer 321 can be broken down into 300 + 20 + 1. The 3 is in the hundreds place. The two in the tenths place and the 1 is in the ones place. Confused? Let’s look at this a different way.
Ancient Babylonians used base 60 instead of base 10. Hence 60 Seconds in a minute and 360 degrees in a circle.
Beyond base 10 and base 2
Let’s recall some basic math facts. Consider the number 22 we say that the number 2 is raised to the 2nd power or that 2 is squared. The raised number is called a superscript and is a nice notation to say the number is multiplied by itself. This translates to 2*2 = 4. Another key fact to recall that a superscript of 0 always equals 1.
With our based 10 system, using superscripts, we can now write numbers in a similar decomposition as the 321 example above.
Ex 1: 321 = 3 * 102 + 2 * 101 + 1 * 100
Ex 2: 111 = 1 * 102 + 1 * 101 + 1 * 100
Ex 3: 555 = 5 * 102 + 5 * 101 + 5 * 100
Base 2 Binary Math
Why in the world are we discussing grade school math and what does this have to do with computers and hacking? Well, computers really only understand one and off, 1 and 0, true or false. With that in mind, hopefully it is clear we must understand how we represent our everyday numbers so we can build different number systems. Let’s now build the famous base 2 number system often called binary.
To construct our base two number system, we now only have 2 numbers, instead of 10 (0-9) to work with, that is we can choose between 1 or 0 for each place. It is customary in binary to write 4 or 8 number places out.
To construct our base 2 system instead of 10 we use the number 2 to a power. For example 1 * 20 or 0 * 20 is So lets look at some examples to cement this new idea.
Ex 4: 1111 = 1* 23 + 1 * 22 + 1 * 21 + 1 * 20 or 8 + 4 + 2 + 1 = 15
Ex 5: 1010 = 1* 23 + 0 * 22 + 1 * 21 + 0 * 20 or 8 + 0 + 2 + 0 = 10
Ex 6: 1000 = 1* 23 + 0 * 22 + 0 * 21 + 0 * 20 or 8 + 0 + 0 + 0 = 8
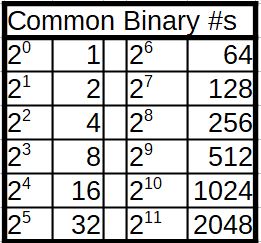
The smallest binary digit is a bit, a 1 or 0.
A byte is 8 bits 28 b
A Kilo is 1024 bytes = 210 B
A Mega is 1048576 = (210)2 = 10242K
A Gig is 1073741824 = = (210)3 = 10243M
Applications – Internet Protocol Addresses
The IP address can be represented in binary, in fact, those that have studied advanced networking, are aware of the pains of subnetting.
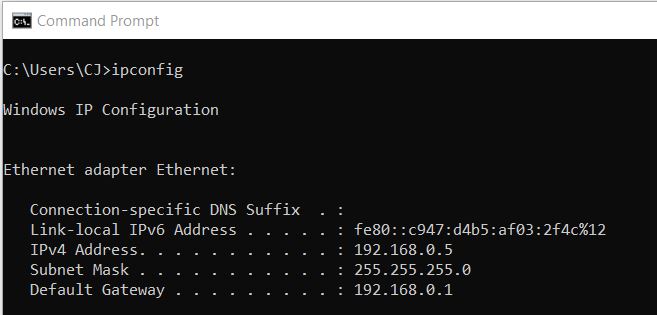
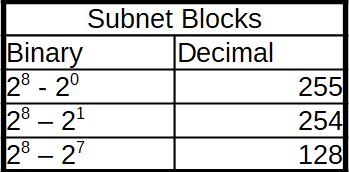
The tables below shows a graphical representation of what network administrators may use when designed routed and switched networks.

Applications – Pictures
The term RGB or Red Green Blue can be used to implement a color scheme. The values 0-255 can be used as a scale for each color and ultimately represent any shade. In a picture this can be used to create 16.7 million colors.
Applications – Digital Logic Circuits
Digital circuits use positive or negative voltage levels that can be represented by either a logic level “1” or a logic level “0”. That is, either ON or OFF or TRUE or FALSE. In fact in some computer programming languages 1 is used interchangably for true and 0 for false.
I hope this tutorial was not too dry and that it helped cement the fact that binary is critical to computers, and an understanding is necessary to represent memory, digital display and the logic of the processor.